GTM
Wednesday, August 05, 2020
Konstruksi Geometri
Dalam menggambar suatu mesin atau komponennya, tukang gambar sering menggunakan konstruksi geometris untuk membantu dalam menyelesaikannya. Konstruksi geometris yang sering digunakan antara lain: garis, sudut, lingkaran, busur, ellips, segi banyak, dan lain-lain.
Penggunaan konstruksi geometris dalam gambar teknik mesin dengan maksud agar hasil gambar yang didapat lebih baik. Pembuatan ellips yang dibuat dengan bantuan lingkaran hasilnya akan lebih akurat dan pantas dari pada yang dibuat dengan perkiraan saja. Untuk itulah seorang juru gambar harus menguasai cara pembuatan konstruksi geometris ini.
(1) Membagi Garis Sama Panjang
Caranya :
(a). Gambarkan garis A-B (sembarang) !
(b). Lingkarkan jangka dengan jari-jari r1, dengan titik A sebagai pusatnya !
(c). Dengan tidak merubah jangka (r1 = r2), lingkarkan r2tersebut dengan
titik pusat di B, sehingga berpotongan di C dan D !
(d). Tarik garis tipis dari C ke D hingga memotong garis A-B di E, sehingga
AE = EB !
Gb. 1.29 Membagi garis A – B sama besar
(2) Membagi Garis Menjadi n Bagian Sama Besar
Caranya : lihat gambar 1.30
(a) misalkan n = 15 bagian sama besar !
(b) tentukan garis AB dan gambarkan !
(c) tarik garis pertolongan dari titik A ke bawah dengan sudut sembarang !
(d) tentukan jangka dengan jari-jari r = A-1 !
(e) buatlah garis batas dengan jangka yang mempunyai jari-jari r tersebuit dengan titik pusat berturut-turut A-1, 2, 3, … , sampai dengan 14 !
(f) hubungkan titik B dengan 15 (sebagai garis penutup) !
(g) buatlah garis sejajar (menggunakan mistar satu pasang) melalui 1, 2, 3, …, dan seterusnya yang sejajar dengan garis penutup, hingga didapat perpotongan garis di C, D, E, dan seterusnya ! Diperoleh AC = CD = DE = EF = FG dan seterusnya.

(3) Membagi Sudut Sama Besar
Caranya :
a) Buat sudut BAC yang akan dibagi dua sama besar !
b) Tentukan r1 dengan jangka dan lingkarkan dengan titik pusat di A, hingga memotong garis AB di D dan garis AC di E !
Gb. 1.31 Membagi sudut sama besar
c) Tentukan r2 (sembarang) dan lingkarkan dengan titik pusat di D dan E, sehingga berpotongan di F !d) Hubungkan garis dari titik A ke titik F !
Diperoleh sudut BAF = sudut FAC.
(4) Membagi Sudut Menjadi Tiga Bagian
Caranya : lihat gambar 1.32
a) Gambarkan sudut BAC yang akan dibagi sudutnya menjadi tiga bagian sama besar !
b) Perpanjang AC ke kiri sebagai garis pertolongan !
c) Tentukan r1 (sembarang) dan lingkarkan dengan titik pusat di A hingga berpotongan di E, D, dan F !
d) Tentukan r2 = 2 . r1 dan lingkarkan dari titik pusat E dan F hingga berpotongan di G !
e) Tarik garis bantu dari D ke G hingga berpotongan di H !
f) Bagi tiga panjang H-E hingga didapat 1’ dan 2’ !
g) Tarik garis dari G ke 1’ dan G ke 2’ hingga didapat I dan J pada lingkaran !
h) Hubungkan I dan J dengan A, sehingga didapat 3 sudut sama besar !
Gb. 1.32 Membagi sudut menjadi 3 bagian
Caranya :
1) tentukan garis OA mendatar !
2) tentukan r (sembarang) dan lingkarkan busur dengan titik pusat di O !
3) Pindahkan jangka yang berjari-jari r 9tidak diubah) dengan titik pusat di B hingga berpotongan di C !
4) Hubungkan O dengan C !
Diperoleh sudut AOC = 60derajat
Gambar 1.33 Membagi sudut 60derajat dan 30derajat
(6) Membuat Sudut 30 derajat
Caranya :
a) buat garis OA mendatar !
b) tentukan jari-jari r dan lingkarkan dengan titik pusat di O hingga berpotongan di B !
c) pindahkan titik pusatnya ke B hingga berpotongan di C !
d) pindahkan kembali titik pusat ke B dan C hingga berpotongan di E !
e) hubungkan O dengan E hingga didapat AOE mempunyai sudut 30derajat !
(7) Membuat Sudut 90 derajat
Cara I :
a) tarik garis AO dan perpanjang ke kiri !
b) tentukan r1 dan lingkarkan dengan titik pusat di O hingga berpotongan di B dan C !
c) tentukan r2 (sembarang) dan lingkarkan dengan titik pusat di B dan C hingga berpotongan di D !
d) hubungan O dengan D maka sudut AOD = 90derajat !
Cara II :
a) tarik garis OA mendatar
b) tentukan r (sembarang) dan lingkarkan dengan titik pusat di O hingga berpotongan di B !
c) pindahkan lingkaran yang berjari-jari r ke titik pusat B dan berpotongan di C !
d) pindahkan kembali ke titik pusat C dan berpotongan di D !
e) putarkan kembali dengan titik pusat di D dan C hingga berpotongan di E !
f) hubungkan O dengan E maka sudut AOE = 90derajat
Gb. 1.34 Membuat sudut 90derajat
(8) Membuat Sudut 45 derajat
Caranya :
1) Buat garis OA mendatar dan perpanjang ke kiri !
2) Tentukan r1 dan lingkarkan dengan titik pusat di O hingga berpotongan di B dan C !
3) tentukan r (sembarang) dan putar dengan titik pusat di B dan C hingga berpotongan di D !
4) tarik garis bantu dari O ke D hingga berpotongan dengan busur lingkaran r1 di E !
5) tentukan r2 (sembarang) dan lingkarkan dengan titik pusat di B dan E hingga berpotongan di F
6) hubungkan O dengan F sehingga didapat sudut AOF = 45derajat !
Gb. 1.35 Membuat sudut 450
(9) Membuat segi empat beraturan
Caranya :
1) Tarik garis sumbu AB (mendatar) !
2) Lingkarkan jangka dengan r = ½ sisi segiempat yang dikehendaki (lingkaran bertitik pusat di O) !
3) Lingkarkan busur dengan jari-jari R (sembarang) dan bertitik pusat di A dan B, sehingga didapat titik C dan D !
4) Hubungkan C dan D melalui O (sehingga didapat sumbu tegak), memotong lingkaran di E dan F !
Gb. 1.36 Segi empat beraturan
5) Tarik garis sejajar AB melalui E dan F !6) Tarik garis sejajar EF melalui A dan B, hingga berpotongan di titik G, H, I, dan J !
Maka segiempat GHIJ adalah segiempat beraturan.
(10) Segi lima beraturan
Gb. 1.37 Segi lima beraturan
Caranya :
1) Lingkarkan jangka yang berjari-jari r1 dengan titik pusat di O !
2) Tarik garis sumbu mendatar melalui O hingga berpotongan dengan lingkaran di A dan B !
3) Lingkarkan jangka yang berjari-jari r dengan titik pusat di A dan B hingga berpotongan di C !
4) Tarik garis dari O ke C hingga memotong lingkaran di G !
5). Lingkarkan jangka yang berjari-jari r1 dari titik pusat B, hingga memotong lingkaran di titik D dan E; lalu hubungkan D dengan E hingga memotong sumbu AB di titik F !
6) Ukurkan jangka dari F ke G (r2 = FG) dan lingkarkan r2tersebut dengan titik pusat di F hingga memotong sumbu AB di H !
7) Ukur GH dengan jangka (GH = r3) ini merupakan sisi segilima beraturan !
8) Pindahkan r3 berturut-turut dengan titik pusat di I, J, K, dan L !
9) Hubungkan G dengan I, I dengan J, j dengan E, E dengan L, dan L dengan G, sehingga didapat segilima beraturan !
(11) Segi enam Beraturan
Caranya :
1) Tentukan jari-jari r dan lingkarkan dengan titik pusat di O !
2) Tarik garis sumbu mendatar melalui O hingga berpotongan dengan lingkaran di A dan B !
3) Lingkarkan jangka yang berjari-jari r tadi (tidak dirubah) dengan titik pusat di A dan titik pusat di B, hingga didapat titik potong dengan lingkaran di C, D, E, dan F !
4) hubungkan A dengan D, D dengan E, E dengan B, B dengan F, F dengan C, dan C dengan A, hingga didapat segienam beraturan !
Gbr. 1.38 Segi enam beraturan
(12) Segi tujuh beraturan
Gb. 1.39 Segi tujuh beraturan
Caranya :
1) tentukan jari-jari r1 dan lingkarkan dengan titik pusat di O !
2) tarik garis mendatar (sumbu) melalui O hingga didapat titik potong A dan B !
3) buat garis tegak lurus AB melalui O hingga berpotongan di P dan perpanjang ke atas !
4) dengan cara lukisan, garis AB dibagi tujuh bagian sama besar, hingga didapat 1’, 2’, 3’, 4’, 5’, 6’, dan 7’ !
5) ukur dengan jangka dari A ke 1’ (A1’ = r2) dan lingkarkan r2 tersebut dengan titik pusat di A hingga berpotongan dengan perpanjangan AB di E !
6) ukur dengan jangka dari O ke E (OE=r3) dan lingkarkan r3tersebut dengan titik pusat di O hingga memotong garis perpanjangan OP di G !
7) tarik garis dari E ke G hingga memotong lingkaran di titik H !
8) ukur dengan jangka dari H ke 3’, ini merupakan sisi segitujuh !
9) pindahkan s=H-3’ ke P-Q, Q-R, R-S, S-T, T-U, dan seterusnya hingga didapat segitujuh beraturan !
(13) Segi-n Beraturan
Untuk membuat segi-n beraturan dengan cara pendekatan, dapat dilakukan/dilukiskan seperti cara melukis segitujuh beraturan; perbedaannya hanya terletak dalam pembagian garis tengahnya, yaitu garis tengahnya dibagi dalam n bagian sama besar. Misalnya untuk segi-11, maka garis tengahnya dibagi menjadi 11 bagian. Sedangkan untuk menentukan panjang sisi r selalu diambil jarak dari 3’ ke titik H pada gambar segi-7 atau titik F pada contoh segi-n = 11 untuk gambar berikut.
Untuk membuat segi-n beraturan ini, selain dapat dilukis dengan menentukan lingkaran pembantu terlebih dulu, dapat juga dilukis dengan menentukan panjang sisi segi-n terlebih dahulu (lihat gambar 1.40).
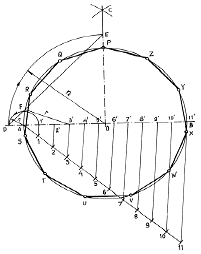
(14) Elips
Elips dengan dua lingkaran pertolongan sepusat dapat dilukiskan dengan langkah-langkah seperti berikut :
a) tentukan titik pusat lingkaran O !
b) buat lingkaran kecil dengan jari-jari r dan lingkaran besar dengan jari-jari R yang titik pusatnya di
titik O’!
c) bagi lingkaran tersebut menjadi 16 bagian sehingga pada lingkaran besar terdapat titik potong A, B, C, …, P dan pada lingkaran kecil terdapat titik potong 1, 2, 3, 4, 5, 6, …, 16!
d) Buat garis horizontal dari titik potong 2, 3, 4, ke kanan, garis horizontal dari titik potong 6, 7, 8, ke
kiri, 10, 11, 12 ke kiri, dan 14, 15, 16 ke kanan!
e) Buat garis vertikal dari I, E, dan K, hingga berpotongan di 1’, 2’, dan 3’!
f) Buat garis vertikal dari M, G, dan O, hingga berpotongan di 6’, 7’, dan 8’, sedangkan 5 = 5’!
g) Buat garis vertikal dari titik J, F, dan L, begitu juga titik N, H, dan P, hingga berpotongan dengan
garis mendatar 9 = 9’, 10’, 11’, 12’, 13 = 13’, 14’, 15’, dan 16’!
h) Hubungkan titik A’ dengan 2’, 3’, 4’, …, 16’ menggunakan mal busur, hingga mendapatkan elips
yang diinginkan!
Rangkuman
1) Gambar merupakan sebuah alat untuk menyatakan maksud terutama bagi orang-orang teknik. Gambar teknik berfungsi sebagai : a) penyampaian informasi, b) pengawetan dan penyimpanan, c) penuangan gagasan dan pengembangan.2) Standar gambar teknik merupakan suatu keseragaman yang telah disepakati bersama dengan tujuan untuk menghindari salah pengertian dalam komunikasi teknik.
3) Untuk dapat menggambar teknik dengan baik diperlukan alat-alat gambar yang lengkap, cara menggunakan alat gambar serta membersihkan dan menyimpan alat-alat gambar dengan baik. Alat-alat gambar yang biasa digunakan antara lain: a) kertas gambar, b) pensil, pena atau rapido, c) macam-macam mistar, d) jangka, e) macam-macam mal, f) penghapus, g) papan gambar dan meja gambar, h)mesin gambar.
4) Dalam gambar teknik huruf-huruf, angka-angka dan lambang-lambang dipergunakan untuk memberi ukuran-ukuran, catatan-catatan, judul, dan sebagainya. Huruf dan angka harus jelas, seragam dan bentuk huruf harus mudah ditulis dan dibaca. Penulisan huruf dan angka biasanya dalam bentuk tegak dan bentuk miring. Sedangkan tipe huruf dan angka berdasarkan perbandingan tinggi huruf dan tebal huruf adalah tipe huruf A (d=h/14) dan tipe huruf B (d=h/10).
5) Macam-macam garis pada gambar teknik antara lain: a) garis tebal kontinu, b) garis tipis kontinu, c) garis tipis kontinu bebas, d) garis gores tebal, e) garis bergores tipis, f) garis bergores tipis yang dipertebal pada ujung-ujungnya. Masing-masing jenis garis tersebut mempunyai kegunaan sendiri-sendiri.
6) Gambar konstruksi geometri diperuntukkan melatih ketrampilan dalam menggunakan peralatan gambar. Konstruksi geometri antara lain: a) membagi garis, b) membagi dan membuat sudut, c) menggambar segi-segi dan elips.